
Thus, the problem of maximizing the possible number of rearrangements W, defined by Eq. This quantity, S, is called the information entropy. S = − ∑ i = 1 n p i log p i, (2)where p i = N i/ N is the fractional number that particles are occupied at the state i. We take this limiting procedure only after the standard discretized formulation is completed below.

On the other hand, in most of the physical applications, it is more convenient to take the limit of n → ∞. A discretized formulation with a finite number n of states is crucial for calculating the number of possible rearrangements under a given distribution in a convenient manner, as seen immediately below. In the PSD problem, more precisely, we may define such possible states by bins defined by the range of the particles sizes with D i = D min + ( i − 1)Δ D for i = 1, …, n in terms of the minimum D min and the maximum D max particles sizes of the interest with the bin size defined by Δ D = ( D max − D min)/ n. In the other problems, these can be a set of physical values, or the energy states, etc. In the case of the PSD problem, the possible states are a set of the values for the particles sizes. The goal of the problem is to define a distribution of “particles” over all these possible states. In some general applications, we may also need to consider a limit of N → ∞. Here, the “particles” are not necessarily particles in physical sense, but it may be reinterpreted in a more abstract manner in considering more general distribution problems outlined in the last section.
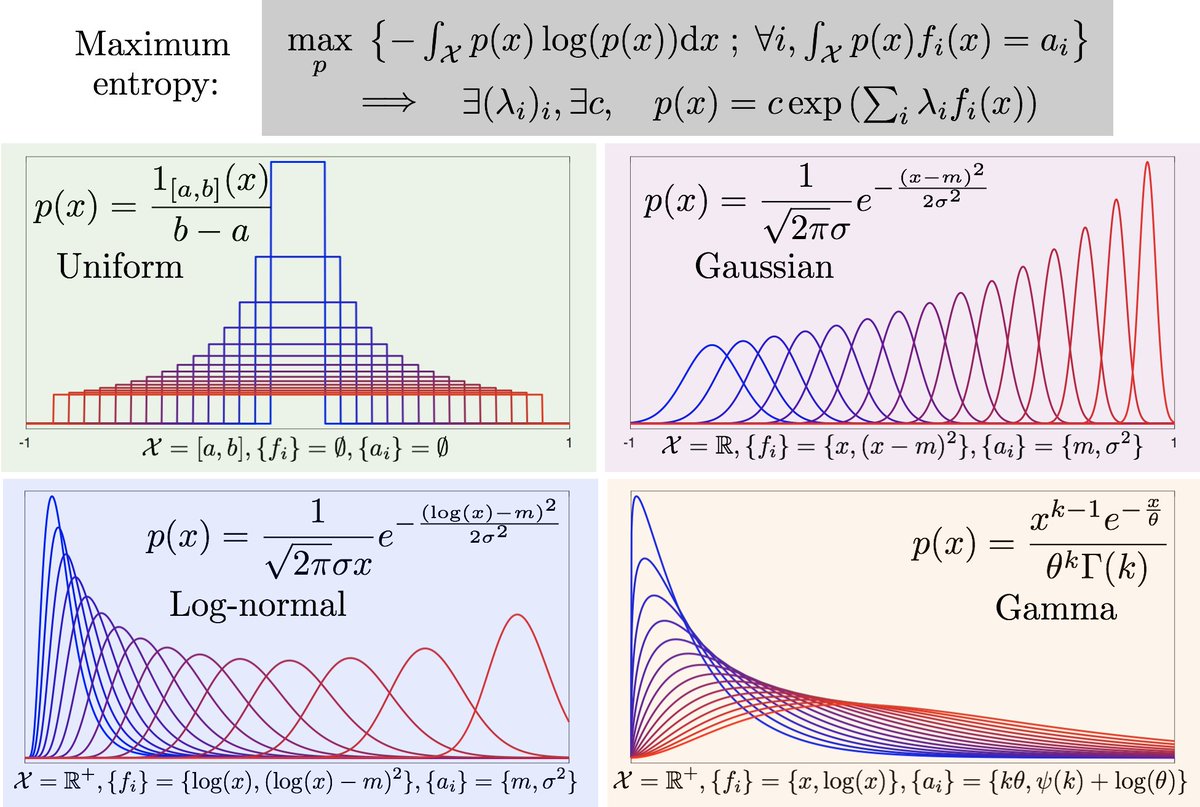
Let us consider a system consisting of N “particles.” We assume that these “particles” can take n possible states. The maximum entropy principle formulates the problem in the following manner. For this reason, a certain caution is required in applying this principle to any scientific problems. However, as already stated, applicability of this principle is hardly obvious to a given physical problem, although our experience suggests a wide applicability of this principle (cf. Intuitively speaking, the methodology would provide the statistically most likely distribution. The distribution is sought over all the possible distribution forms with the latter constrained by a set of integral constraints, as more explicitly formulated in the next section. The principle simply seeks a distribution that gives the largest possible number of rearrangements of a given number of particles (or any generalizations of such). For example, although it is often remarked in popular books that the principle is only applicable to an equilibrium state, the principle itself does not invoke any notion of “equilibrium.” The notion of “equilibrium” is merely implied, if one wishes to interpret it in such a manner. However, we should also realize that it is merely a mathematical principle, and it is hardly obvious when and how this principle can be applied to physical problems, as the following discussion is going to elucidate. The maximum entropy principle can also be applied to more abstract distributions such as energy spectra (e.g., Robert and Sommeria 1991 Verkley 2011 Verkley and Lynch 2009 Verkley et al. Another distribution problem is found in determining distributions of variables in subgrid scale (e.g., Larson 2004): a notable problem is a distribution of the total water, which is required for determining a fractional area occupied by clouds over a given grid box. The particle size distribution (PSD) of hydrometeor as considered by Wu and McFarquhar (2018, and see further extensive references therein) is a particular example of a distribution problem. The maximum entropy is a general principle for determining the most likely “distribution.” Here, the “distribution” can be interpreted in a general manner as much as possible.


 0 kommentar(er)
0 kommentar(er)
